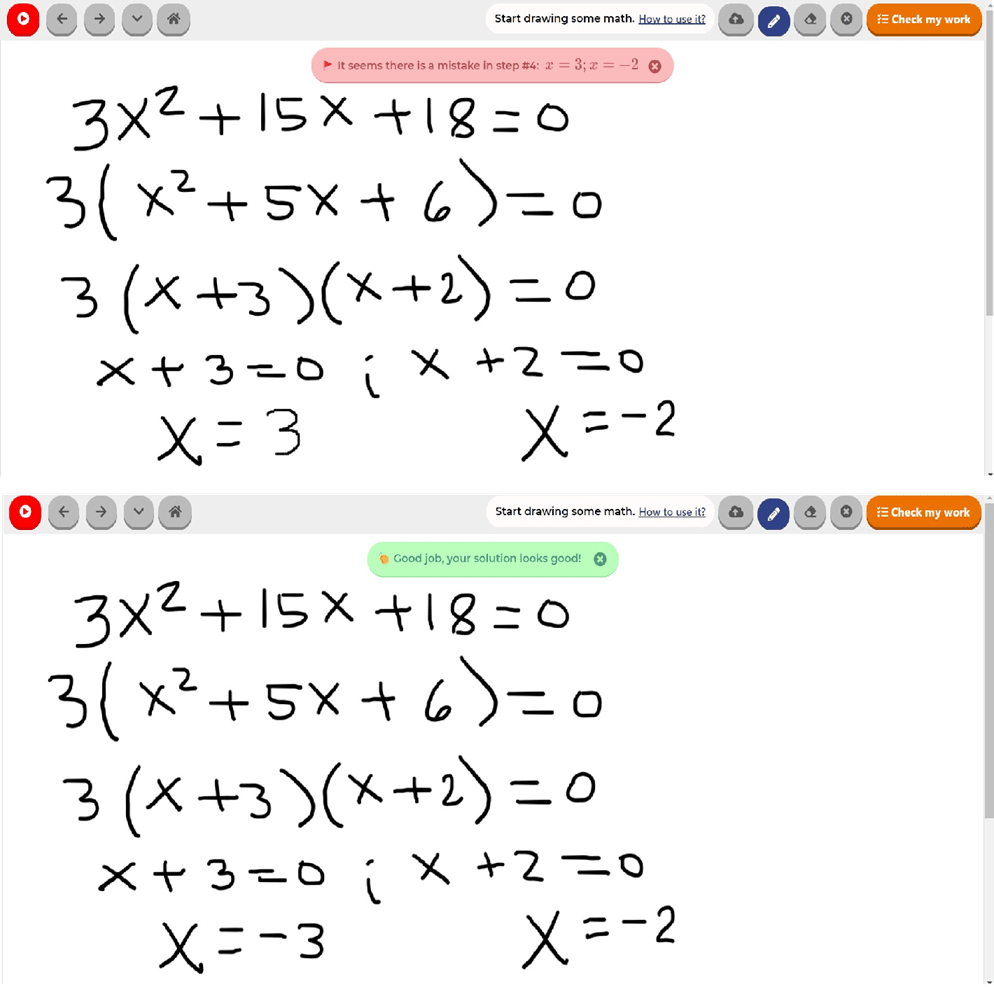
Final answer to the problem
Step-by-step Solution
Learn how to solve proving trigonometric identities problems step by step online. Prove the trigonometric identity (sin(x)+cos(x))^2-1=2sin(x)cos(x). Starting from the left-hand side (LHS) of the identity. Expand the expression \left(\sin\left(x\right)+\cos\left(x\right)\right)^2 using the square of a binomial: (a+b)^2=a^2+2ab+b^2. Applying the pythagorean identity: \sin^2\left(\theta\right)+\cos^2\left(\theta\right)=1. Subtract the values 1 and -1.