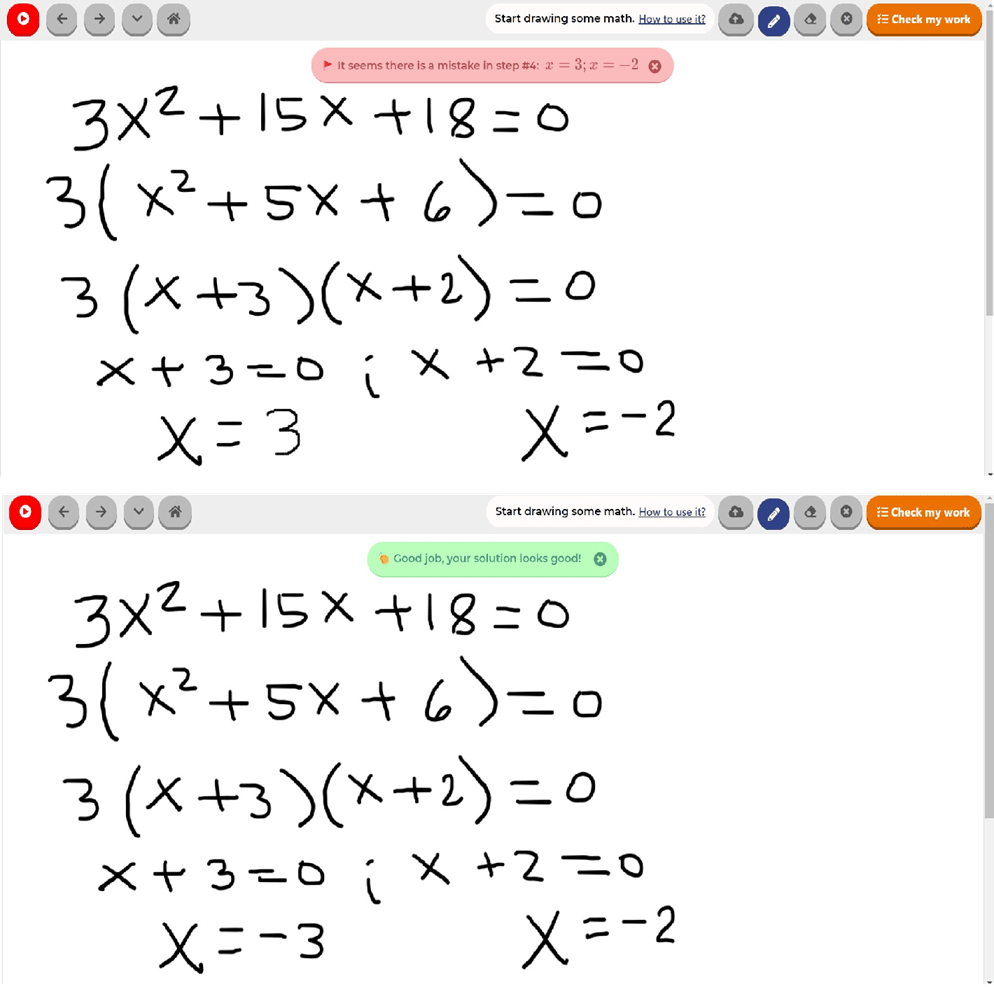
Final answer to the problem
Step-by-step Solution
Learn how to solve proving trigonometric identities problems step by step online. Prove the trigonometric identity (sec(x)^2+tan(x)^2+1)cos(x)^2=2. Starting from the left-hand side (LHS) of the identity. Applying the trigonometric identity: 1+\tan\left(\theta \right)^2 = \sec\left(\theta \right)^2. Combining like terms \sec\left(x\right)^2 and \sec\left(x\right)^2. Applying the secant identity: \displaystyle\sec\left(\theta\right)=\frac{1}{\cos\left(\theta\right)}.