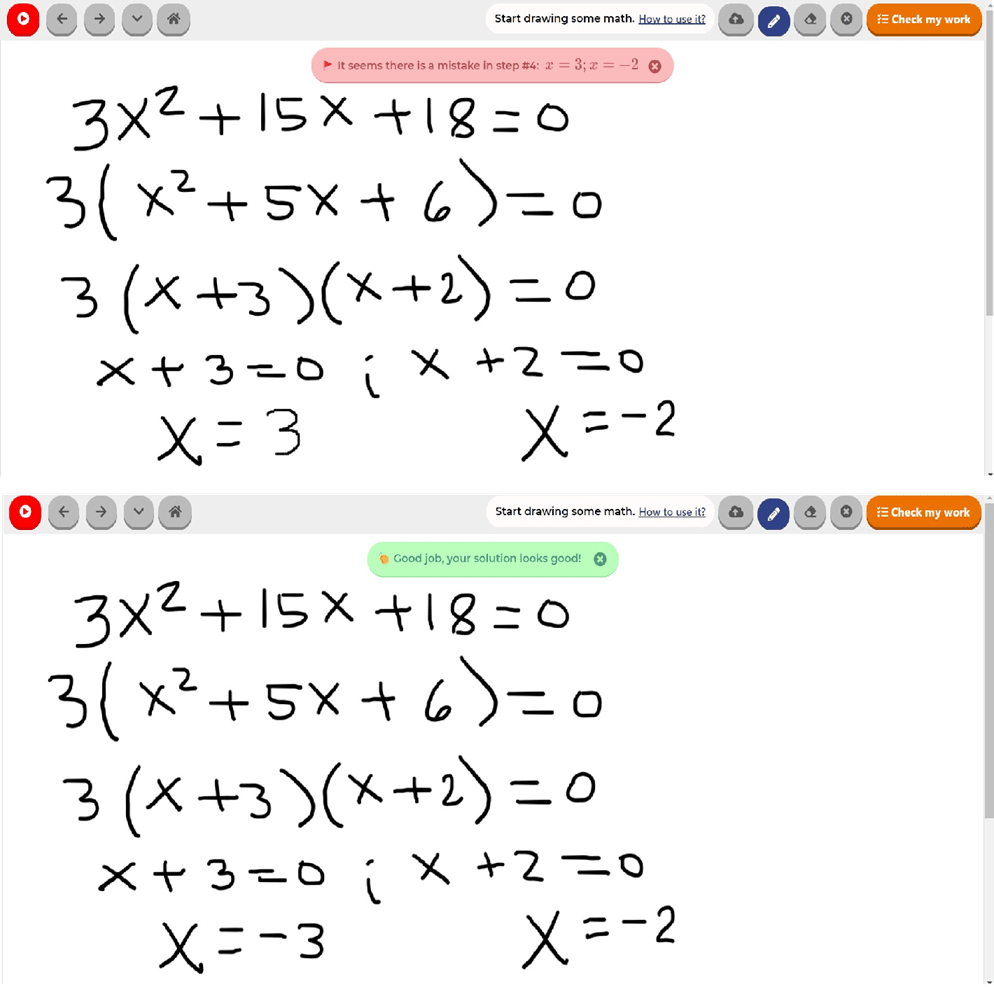
Final answer to the problem
Step-by-step Solution
Learn how to solve special products problems step by step online. Expand the logarithmic expression log(((1000*x)^4*(x+-7)^(1/2))/((x^2+-49)^3)). The difference of two logarithms of equal base b is equal to the logarithm of the quotient: \log_b(x)-\log_b(y)=\log_b\left(\frac{x}{y}\right). Use the product rule for logarithms: \log_b\left(MN\right)=\log_b\left(M\right)+\log_b\left(N\right), where M=\left(1000x\right)^4 and N=\sqrt{x-7}. Using the power rule of logarithms: \log_a(x^n)=n\cdot\log_a(x). Using the power rule of logarithms: \log_a(x^n)=n\cdot\log_a(x).