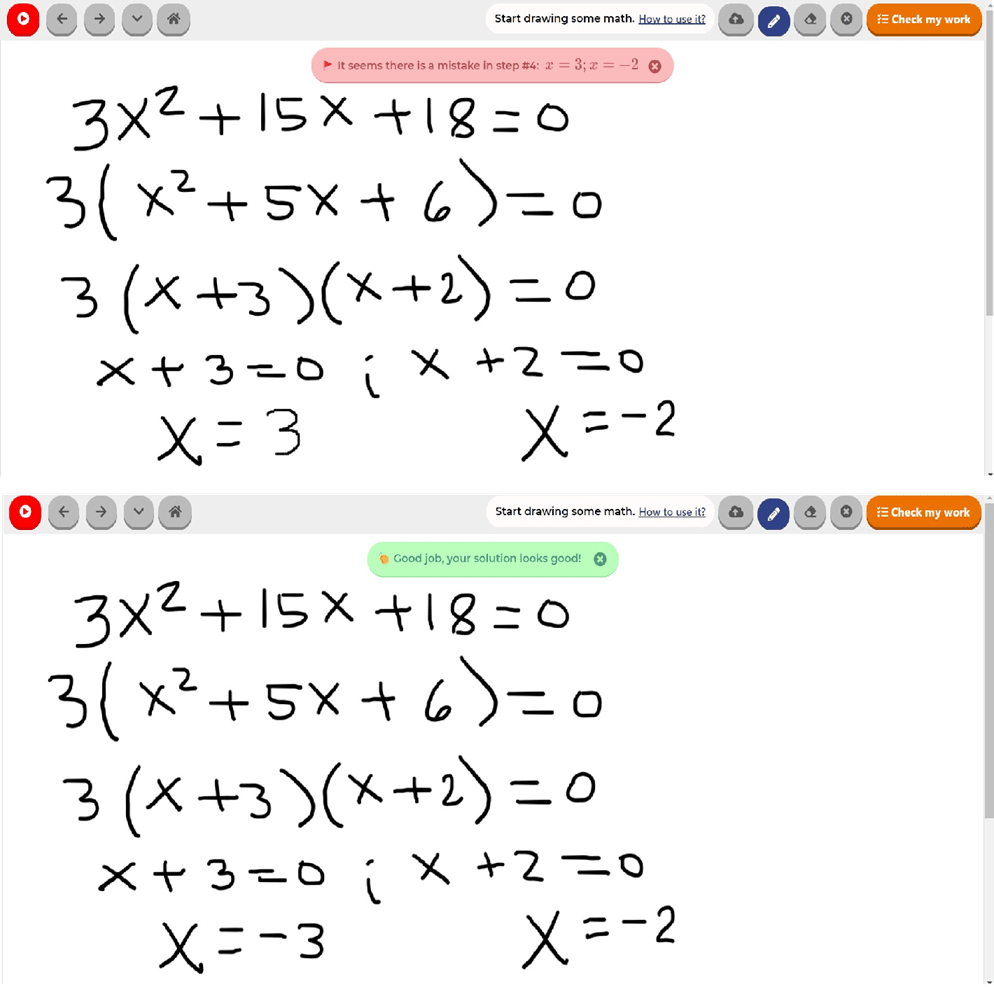
Final answer to the problem
Step-by-step Solution
Learn how to solve rational equations problems step by step online. Solve the rational equation y=(((x+1)^10)/((3x-5)^9))^(1/2). The power of a quotient is equal to the quotient of the power of the numerator and denominator: \displaystyle\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}. Simplify \sqrt{\left(3x-5\right)^9} using the power of a power property: \left(a^m\right)^n=a^{m\cdot n}. In the expression, m equals 9 and n equals \frac{1}{2}. Simplify \sqrt{\left(x+1\right)^{10}} using the power of a power property: \left(a^m\right)^n=a^{m\cdot n}. In the expression, m equals 10 and n equals \frac{1}{2}. Simplify \sqrt{\left(3x-5\right)^9} using the power of a power property: \left(a^m\right)^n=a^{m\cdot n}. In the expression, m equals 9 and n equals \frac{1}{2}.