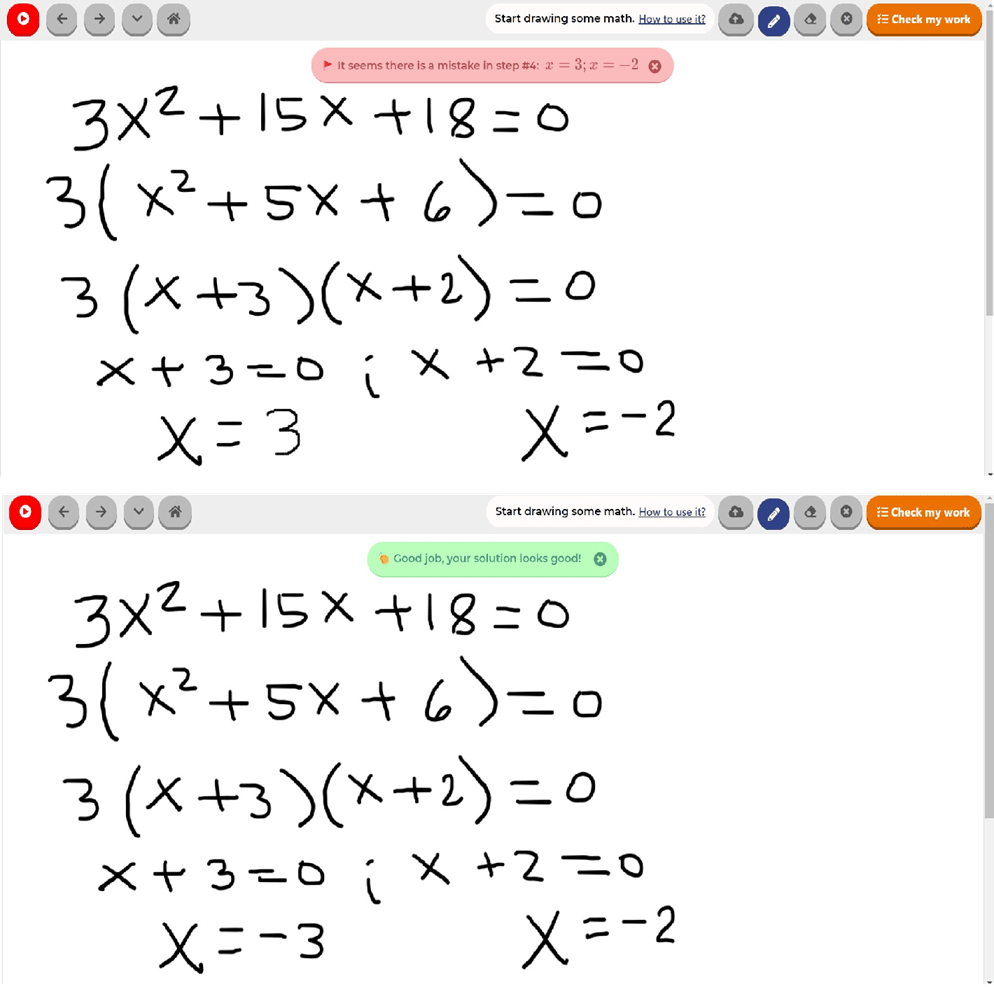
Final answer to the problem
$m\left(x\right)=x^{\left(\frac{1}{3}n-\frac{2}{3}+\frac{1}{2}n-\frac{3}{2}-\frac{1}{6}n+\frac{1}{6}\right)}$
Got another answer? Verify it here!
Step-by-step Solution
Learn how to solve factorization problems step by step online. Simplify the expression m(x)=(x^(n-2)^(1/3)x^(n-3)^(1/2))/(x^(n-1)^(1/6)). Simplify \sqrt[6]{x^{\left(n-1\right)}} using the power of a power property: \left(a^m\right)^n=a^{m\cdot n}. In the expression, m equals n-1 and n equals \frac{1}{6}. Simplify \sqrt[3]{x^{\left(n-2\right)}} using the power of a power property: \left(a^m\right)^n=a^{m\cdot n}. In the expression, m equals n-2 and n equals \frac{1}{3}. Simplify \sqrt{x^{\left(n-3\right)}} using the power of a power property: \left(a^m\right)^n=a^{m\cdot n}. In the expression, m equals n-3 and n equals \frac{1}{2}. When multiplying exponents with same base we can add the exponents.
Final answer to the problem
$m\left(x\right)=x^{\left(\frac{1}{3}n-\frac{2}{3}+\frac{1}{2}n-\frac{3}{2}-\frac{1}{6}n+\frac{1}{6}\right)}$
