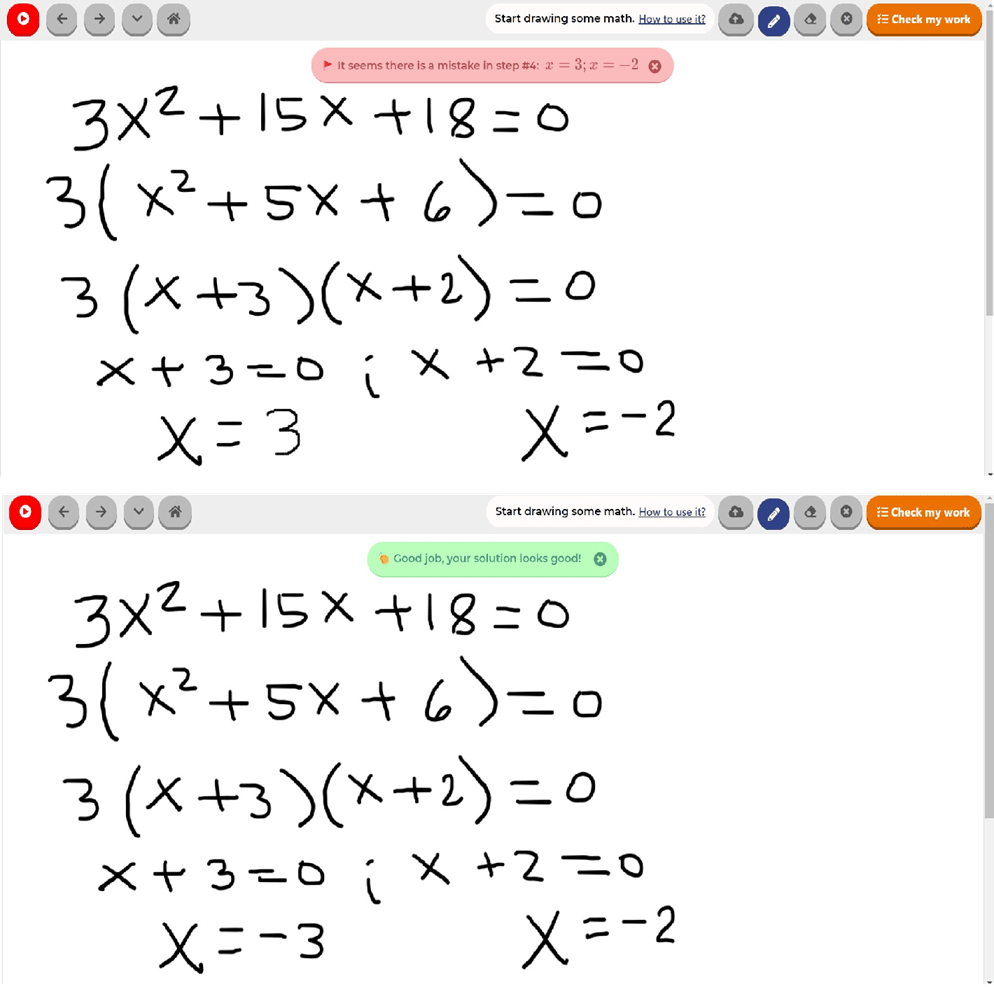
Final answer to the problem
Step-by-step Solution
How should I solve this problem?
- Prove from RHS (right-hand side)
- Prove from LHS (left-hand side)
- Express everything into Sine and Cosine
- Exact Differential Equation
- Linear Differential Equation
- Separable Differential Equation
- Homogeneous Differential Equation
- Integrate by partial fractions
- Product of Binomials with Common Term
- FOIL Method
- Load more...
Starting from the right-hand side (RHS) of the identity
Using the sine double-angle identity: $\sin\left(2\theta\right)=2\sin\left(\theta\right)\cos\left(\theta\right)$
Simplify the fraction $\frac{2\sin\left(x\right)\cos\left(x\right)}{\sin\left(x\right)}$ by $\sin\left(x\right)$
Combine all terms into a single fraction with $\cos\left(x\right)$ as common denominator
When multiplying two powers that have the same base ($\cos\left(x\right)$), you can add the exponents
Combine all terms into a single fraction with $\cos\left(x\right)$ as common denominator
Apply the trigonometric identity: $\cos\left(2\theta \right)$$=2\cos\left(\theta \right)^2-1$
Simplify the product $-(2\cos\left(x\right)^2-1)$
Multiply $-1$ times $-1$
Simplify the product $-(2\cos\left(x\right)^2-1)$
Cancel like terms $2\cos\left(x\right)^2$ and $-2\cos\left(x\right)^2$
Applying the trigonometric identity: $\displaystyle\sec\left(\theta\right)=\frac{1}{\cos\left(\theta\right)}$
Since we have reached the expression of our goal, we have proven the identity